Distance

2025-03-18

Distance

Many of the analyses we perform with high-dimensional data relate directly or indirectly to distance.
Many machine learning techniques rely on defining distances between observations.
Clustering algorithms search of observations that are similar.
But what does this mean mathematically?

The norm

A point can be represented in polar coordinates:

The norm

If \(\mathbf{x} = (x_1, x_2)^\top\), \(r\) defines the norm of \(\mathbf{x}\).

The norm

The point of defining the norm is to extrapolate the concept of size to higher dimensions.
Specifically, we write the norm for any vector \(\mathbf{x}\) as:

\[ ||\mathbf{x}|| = \sqrt{x_1^2 + x_2^2 + \dots + x_p^2} \]

Sometimes convenient to write like this:

\[ ||\mathbf{x}||^2 = x_1^2 + x_2^2 + \dots + x_p^2 \]

The norm

We define the norm like this:

\[ ||\mathbf{x}||^2 = \mathbf{x}^\top\mathbf{x} \]

Distance

Distance is the norm of the difference:

Distance

-We can see this using the definition we know:

\[ \mbox{distance} = \sqrt{(x_{11} - x_{12})^2 + (x_{21} - x_{22})^2} \]

Distance

Using the norm definition can be extrapolated to any dimension:

\[ \mbox{distance} = || \mathbf{x}_1 - \mathbf{x}_2|| \]

Distance

For example, the distance between the first and second observation will compute distance using all 784 features:

\[ || \mathbf{x}_1 - \mathbf{x}_2 ||^2 = \sum_{j=1}^{784} (x_{1,j}-x_{2,j })^2 \]

Distance

Define the features and labels:

mnist <- read_mnist()
x <- mnist$train$images  
y <- mnist$train$labels

x_1 <- x[6,] 
x_2 <- x[17,] 
x_3 <- x[16,]

Compute the distances:

c(sum((x_1 - x_2)^2), sum((x_1 - x_3)^2), sum((x_2 - x_3)^2)) |> sqrt()

[1] 2319.867 2331.210 2518.969

Checks out:

y[c(6,17,16)]

[1] 2 2 7

Distance

In R, the function crossprod(x) is convenient for computing norms.
It multiplies t(x) by x:

c(crossprod(x_1 - x_2), crossprod(x_1 - x_3), crossprod(x_2 - x_3)) |> sqrt()

[1] 2319.867 2331.210 2518.969

Distance

We can also compute all the distances at once:

d <- dist(x[c(6,17,16),]) 
d

         1        2
2 2319.867         
3 2331.210 2518.969

dist produces an object of class dist

class(d)

[1] "dist"

There are several machine learning related functions in R that take objects of class dist as input.

Distance

dist objects are similar but not equal to a matrices.
To access the entries using row and column indices, we need to coerce it into a matrix.

as.matrix(d)[2,3]

[1] 2518.969

Distance

The image function allows us to quickly see an image of distances between observations.

d <- dist(x[1:300,]) 
image(as.matrix(d))

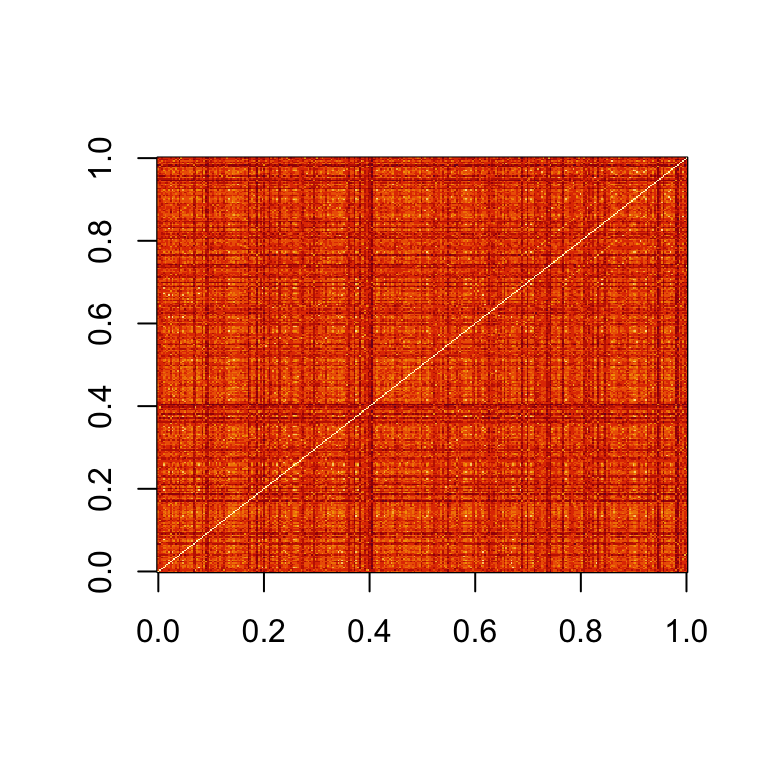
Distance

If we order distance by the labels:

image(as.matrix(d)[order(y[1:300]), order(y[1:300])])

Spaces

Predictor space is a concept that is often used to describe machine learning algorithms.
We can think of all predictors \((x_{i,1}, \dots, x_{i,p})^\top\) for all observations \(i=1,\dots,n\) as \(n\) \(p\)-dimensional points.
The space is the collection of all possible points that should be considered for the data analysis in question, including points we have not observed yet.
In the case of the handwritten digits, we can think of the predictor space as any point \((x_{1}, \dots, x_{p})^\top\) as long as each entry \(x_i, \, i = 1, \dots, p\) is between 0 and 255.

Spaces

Some Machine Learning algorithms also define subspaces.
A commonly defined subspace in machine learning are neighborhoods composed of points that are close to a predetermined center.
We do this by selecting a center \(\mathbf{x}_0\), a minimum distance \(r\), and defining the subspace as the collection of points \(\mathbf{x}\) that satisfy:

\[ || \mathbf{x} - \mathbf{x}_0 || \leq r. \]

Spaces

We can think of this subspace as a multidimensional sphere since every point is the same distance away from the center.
Other machine learning algorithms partition the predictor space into non-overlapping regions and then make different predictions for each region using the data in the region.